En la anterior entrega vimos cómo hay dos intervalos que aparecen con predominancia en la serie armónica, la tercera y la quinta. Así mismo, vimos como una primera aproximación, usando quintas -afinación pitagórica-, para construir todas las notas no daba buen resultado.
La siguente aproximación que tomaremos es buscar los intervalos más puros posibles, entendiendo por más puros como los más cercanos a los intervalos que se producen en la serie armónica.
El temperamento justo o «natural»
Se basa en obtener la afinación de las diferentes notas usando relaciones enteras buscando que sean las mismas notas que aparecen en la serie armónica.
En este sistema, la segunda nota de la escala está a una relación de 9:8 respecto a la tónica, la tercera está a 5:4, la cuarta a 4:3, la quinta a 3:2, la sexta a 5:3 y la séptima, a 15:8
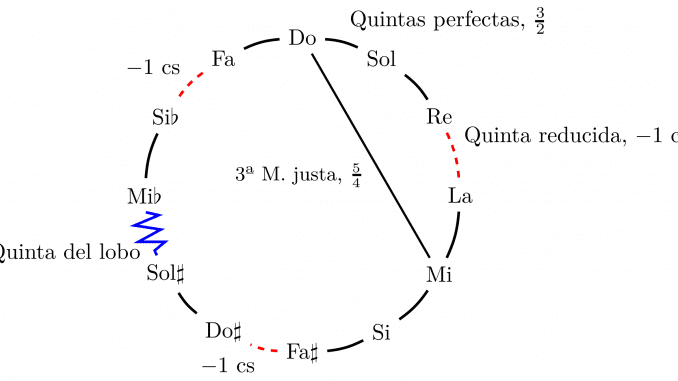
Si se quiere ir construyendo el resto de tonalidades, y que todas las notas encajen en un círculo de quintas, algunas de estas quintas se hacen un poco más pequeñas, concretamente, una de cada cuatro. En este temperamento, las terceras mayores son perfectas, tienen la misma relación de frecuencias que en la serie armónica.
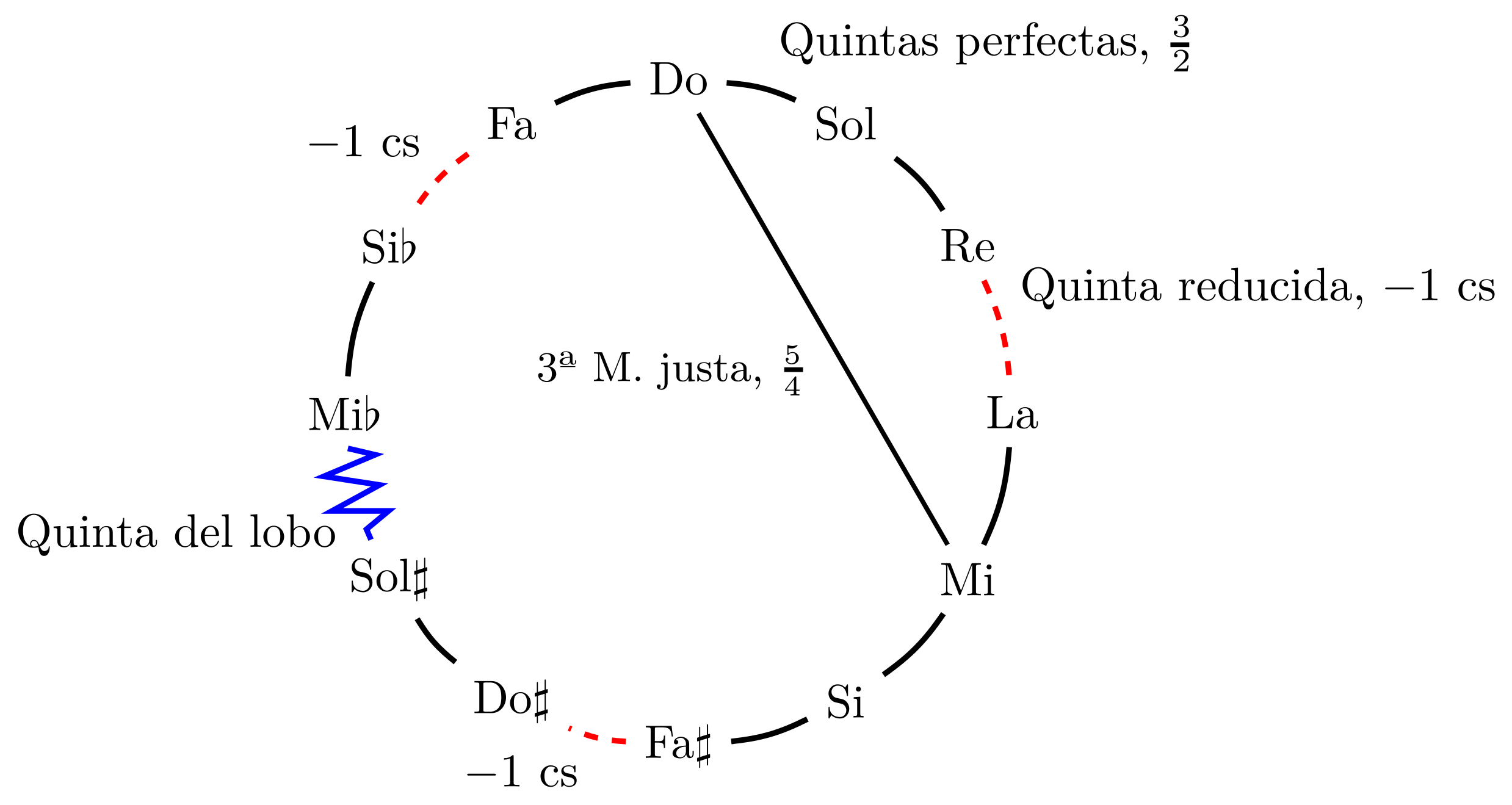
Igual que en el temperamento pitagórico, queda una quinta especialmente pequeña, una quinta del lobo. Por otra parte, al no ser todas las quintas iguales, resulta en intervalos que no son iguales: siguiendo el diagrama anterior, el tono entre Do y Re es algo más grande que el tono entre Sol y La.
En la práctica la afinación justa es problemática, sobre todo en instrumentos de afinación fija (instrumentos de cuerda con trastes, instrumentos de teclado), en los que unas tonalidades se verán favorecidas y otras perjudicadas.
Un ejemplo típico es el que ocurre cuando afinamos una guitarra pulsando un acorde -el típico Mi mayor- hasta que «suena» bien. Cuando tocamos el acorde de Do mayor, que es una tonalidad más bien alejada, no suene sonar bien.
Otros temperamentos, buscando una solución de compromiso
Resumimos lo que hemos avanzado hasta ahora:
- Algunas relaciones de notas nos suenan especialmente bien porque están contenidas en la serie armónica
- Si se construyen las notas siguiendo estas relaciones enteras, no se llega a completar el círculo de intervalos, porque las proporciones de los intervalos principales (quinta, 3:2 y tercera, 5:4) no pueden producir una relación de 2:1 (octava) por mucho que las extendamos.
- Por tanto, algunos de estos intervalos se quedan desafinados, típicamente la quinta entre las notas más alejadas de la tonalidad de Do (quinta del lobo).
Según la música fue avanzando, cada vez era más común cambiar de tonalidad en una obra, o usar tonalidades diversas. Los músicos tuvieron que buscar algún sistema de temperamento que permitiese tener unas intervalos lo más consonantes posibles y que todas las tonalidades fuesen posibles.
Temperamento igual
Este es el temperamento que se utiliza principalmente en la actualidad. El principio matemático es muy sencillo: si tenemos doce notas entre una nota y su octava, dividamos esta octava en doce partes iguales llamadas semitonos. Multiplicando una nota por el factor necesario, obtendremos el siguiente semitono; multiplicando dos veces, el siguiente tono; tres veces, la tercera menor; etc.
Multiplicando una nota doce veces por este factor, tendríamos la octava (f es la frecuencia de la nota y s es el factor que buscamos). Como la octava es el doble de la frecuencia que partimos, podemos escribir:
f·s12 = 2f
Recordando matemáticas básicas, las f se simplifican y se despeja la s
s = 12√2
Es decir, multiplicando la frecuencia de una nota por la raíz 12 de 2 obtenemos el siguiente semitono, y así sucesivamente.
Por ejemplo, la tercera mayor sería (12√2)4, puesto que hay que subir cuatro semitonos para hacer una tercera mayor. Este número es diferenta a la tercera «pura» (5/4). Si repetimos el cálculo para otros intervalos veremos que tampoco coinciden con las frecuencias que corresponderían con el temperamento justo.
En la siguiente tabla copiada de la Wikipedia se comparan los intervalos que se obtienen en este temperamento con los del temperamento justo:
| Intervalo | Valor exacto | Valor decimal |
Centésimas |
Intervalo en temperamento justo |
Centésimos en temp. justo |
Diferencia (%) |
|---|---|---|---|---|---|---|
| Unison (C) | 20⁄12 = 1 | 1 | 0 | 1⁄1 = 1 | 0 | 0 |
| Minor second (D♭) | 21⁄12 = 12√2 | 1.059463 | 100 | 16⁄15 = 1.06666… | 111.73 | -11.73 |
| Major second (D) | 22⁄12 = 6√2 | 1.122462 | 200 | 9⁄8 = 1.125 | 203.91 | -3.91 |
| Minor third (E♭) | 23⁄12 = 4√2 | 1.189207 | 300 | 6⁄5 = 1.2 | 315.64 | -15.64 |
| Major third (E) | 24⁄12 = 3√2 | 1.259921 | 400 | 5⁄4 = 1.25 | 386.31 | +13.69 |
| Perfect fourth (F) | 25⁄12 = 12√32 | 1.33484 | 500 | 4⁄3 = 1.33333… | 498.04 | +1.96 |
| Tritone (G♭) | 26⁄12 = √2 | 1.414214 | 600 | 64⁄45= 1.42222… | 609.78 | -9.78 |
| Perfect fifth (G) | 27⁄12 = 12√128 | 1.498307 | 700 | 3⁄2 = 1.5 | 701.96 | -1.96 |
| Minor sixth (A♭) | 28⁄12 = 3√4 | 1.587401 | 800 | 8⁄5 = 1.6 | 813.69 | -13.69 |
| Major sixth (A) | 29⁄12 = 4√8 | 1.681793 | 900 | 5⁄3 = 1.66666… | 884.36 | +15.64 |
| Minor seventh (B♭) | 210⁄12 = 6√32 | 1.781797 | 1000 | 16⁄9 = 1.77777… | 996.09 | +3.91 |
| Major seventh (B) | 211⁄12 = 12√2048 | 1.887749 | 1100 | 15⁄8= 1.875 | 1088.270 | +11.73 |
| Octave (C) | 212⁄12 = 2 | 2 | 1200 | 2⁄1 = 2 | 1200.00 | 0 |
La gran ventaja de este sistema es que reparte de forma equitativa todas las imperfecciones entre todos los intervalos y las tonalidades. Es un sistema perfecto matemáticamente hablando, puesto que permite construir todas las escalas en las 12 tonalidades sin perjudicar ni favorecer ninguna a tonalidad.
La desventaja es que hay algunos intervalos que se alejan bastante del ideal del intervalo natural. Por ejemplo, las quintas y las cuartas se asemejan bastante a las quintas y cuartas puras, pero las terceras se llegan a alejar bastante.
Estas diferencias son perfectamente audibles, como vamos a comprobar a continuación, en el siguiente clip de vídeo usamos el piano virtual PianoTeq con diferentes temperamentos para tocar algunos intervalos y acordes.

El temperamento igual permite hacer muchas cosas musicalmente, cambiar de tonalidades alejadas, afinar equitativamente instrumentos con trastes o de tecla, etc… pero tiene la desventaja de estas quintas un poco cortas y terceras mayores algo grandes. Hay muchas críticas bien fundamentadas al temperamento igual. El siguiente vídeo es muy ilustrativo:
Resumen de los tres temperamentos vistos:
- Pitagórico: quintas perfectas, terceras muy grandes, no se cierra el círculo de quintas si no se sacrifica una quinta.
- Justo: buenas terceras y quintas, pero algunos intervalos no quedan iguales y según nos vamos a otra tonalidad, suena mal.
- Igual: permite moverse libremente por todas las tonalidades, cierra perfectamente el ciclo de quintas, quintas un poco bajas y terceras algo grandes. Por costumbre, el oído lo acepta relativamente bien.
Hay muchos más temperamentos que buscan la solución de compromiso entre tener intervalos cercanos a los intervalos puros de la serie armónica y poder «cerrar» el círculo de quintas y hacer cambios de tonalidad aceptables, lo veremos en una última entrega.

Dejar una contestacion