Seguimos con la serie de artículos dedicados a la divulgación, en esta entrega vamos a tratar de entender los diferentes sistemas de afinación que existen y sobre todo, de donde vienen.
Empecemos con el fenómeno natural de los armónicos, lo vamos a explicar tomando una cuerda como ejemplo. Al vibrar una cuerda se superponen varias formas o modos de vibración. La vibración básica o fundamental consiste en una onda cuya longitud abarca los dos extremos de la cuerda.
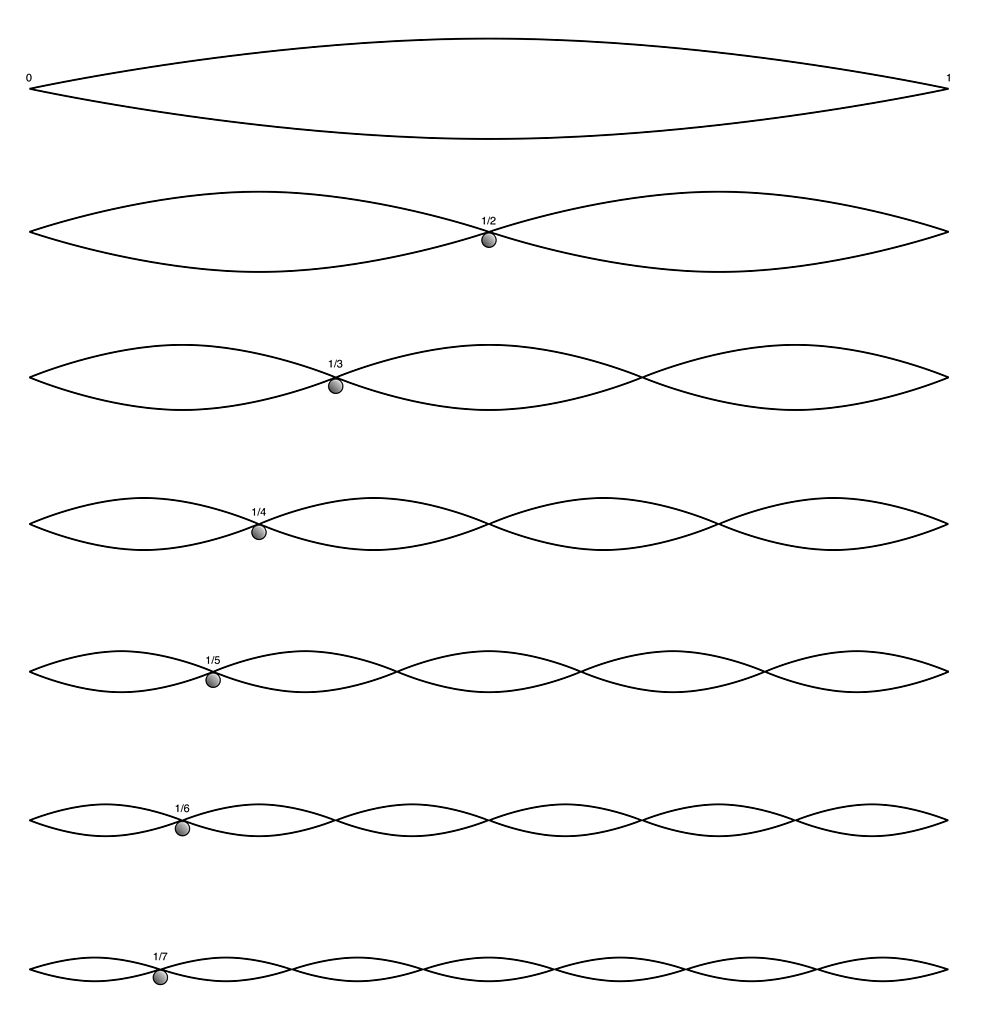
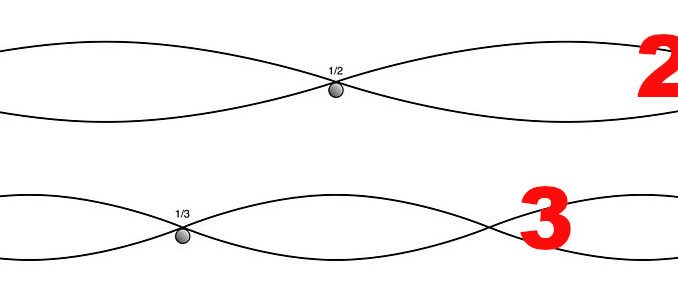
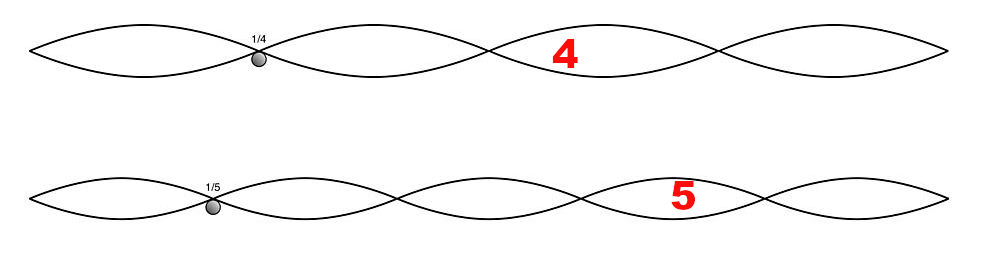
Los siguientes modos de vibración, vibraciones superpuestas toman una fracción entera de la cuerda (la mitad, un tercio, un cuarto, un quinto,…) y producen una vibración con mayor frecuencia superpuesta a la fundamental. Aunque a simple vista estas vibraciones no suelen ser visibles, estos modos de vibración o armónicos sí que son audibles, y la diferente proporción o intensidad relativa de cada uno en una cuerda vibrando determinan el timbre del sonido.
El primer armónico se produce cuando la cuerda se divide en dos partes iguales, la frecuencia de cada una de estas dos partes es el doble de la fundamental. Si nuestra frecuencia fundamental es un La1 (55Hz), la frecuencia de este primer armónico será 110Hz, que corresponde con la nota La2.
El segundo armónico se produce a una frecuencia que es el triple de la del primer armónico, el siguiente a una frecuencia que es el cuadruple…
Los armónicos más bajos son la misma nota octavada, pero según vamos ascendiendo en la serie armónica, vemos que algunos armónicos se corresponden con otras notas (quinta, tercera mayor…)
Según vamos ascendiendo en la serie armónica las notas que van sonando se nos hacen más extrañas porque no coinciden en afinación con los sistemas de afinación que estamos acostumbrados.
Quintas y terceras «puras»
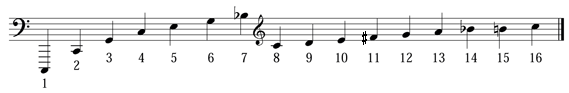
Si observamos la serie armónica, hay dos notas que tienen bastante protagonismo, aparte de la primera. Son la tercera y la quinta.
Suponiendo que estamos en la serie armónica de La, la quinta (Mi) tiene una frecuencia que es 3/2 la del segundo armónico. Por ejemplo, en los armónicos de La, el segundo armónico es La2 (220Hz), el tercer armónico será 330Hz (Mi3) que se corresponde con (3/2)*220.
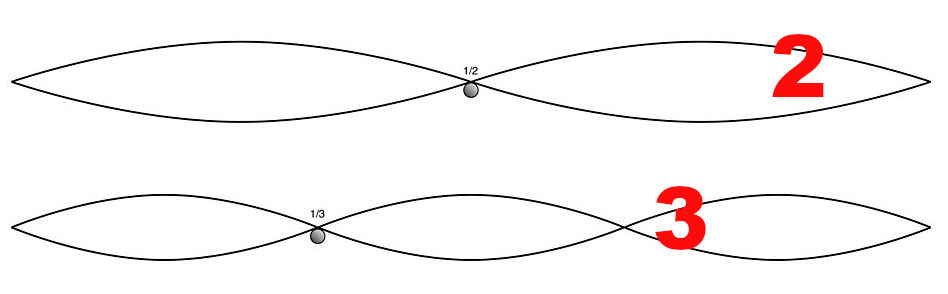
Así mismo, la relación entre el 5º armónico (tercera mayor, Do#) y el 4º armónico (La) es 5/4:
(5/4)* 440 = 550Hz
Estas dos fracciones, 3/2 y 5/4 conforman lo que se suelen llamar los intervalos «puros» o «perfectos» y forman el fundamento de los sistemas de afinación.
En una situación musical en la que tengamos varias notas sonando simultáneamente, si estas notas coinciden con algún armónico de otra nota, se refuerza el sonido y tenemos una sensación de consonancia.
Sin embargo, salvo que nuestra música se reduzca a dos o tres notas, todas dentro de la misma nota fundamental, el sistema va a tener una serie de limitaciones físicas. Lo vemos en unos párrafos.
Construcción de escalas y subdivisión de la octava
Ya hemos visto que de forma natural, los sonidos musicales van repitiendo la misma nota fundamental a diferentes alturas. Este intervalo en nuestro sistema de escalas se llama octava, porque nuestras escalas suelen tener siete notas y a la octava, se repite la nota. El típico Do, Re, Mi, Fa, Sol, La, Si que aprendimos en la escuela es un ejemplo.
¿De dónde viene nuestra escala mayor Do, Re, Mi, Fa, Sol, La, Si?
Hay varias explicaciones, la más habitual implica los armónicos más básicos. La siguiente explicación es, resumidamente, la que ofrece Arnold Schönberg en su «Tratado de armonía»:
Si estamos en Do, las notas que corresponden con los armónicos más bajos son, aparte del mismo Do, las notas Mi (quinto armónico) y Sol (tercer y sexto armónico), con lo que tenemos las notas Do, Mi y Sol.
Dado que Sol tiene bastante peso en el conjunto de armónicos, se puede considerar el mismo Sol como fundamental y sus armónicos más bajos, Si y Re, con lo que tendríamos las notas Sol, Si, Re
Finalmente, podemos pensar en Do no como en fundamental, si no como en la quinta de otra nota, al igual que se consideró Sol como quinta de Do. Dado que Do es la quinta de Fa, se podrían considerar los armónicos mas bajos de Fa, que son La y Do, con lo que tenemos las notas Fa, La y Do.
Resumiento, tenemos los armónicos de Do (Do, Mi, Sol), los de Sol (Sol, Si, Re) y los armónicos de Fa (Fa, La, Do). Reordenando en notas consecutivas llegamos a nuestra conocida escala Do, Re, Mi, Fa, Sol, La, Si.
Afinación pitagórica o por quintas justas
Supongamos que tenemos un instrumento con muchas cuerdas, como un arpa, y queremos afinarlo tomando una cuerda como referencia, afinando el resto en relación a esta. Por simplicidad suponemos que la referencia es una nota Do.
La forma más intuitiva y auditivamente más sencilla es usar quintas para afinar. Podemos pulsar la cuerda Do a dos tercios de su longitud, con lo que salta el tercer armónico, correspondiente a la nota Sol. Con la referencia a este armónico afinamos la cuerda de Sol hasta que al aire suene igual que el tercer armónico que estamos pulsando en la cuerda Do.
Una vez afinada la cuerda Sol, repetimos el proceso para afinar la cuerda Re, tomando como referencia el tercer armónico de la cuerda Sol. Con la cuerda Re afinada, usamos su tercer armónico (La) para afinar la cuerda La. Con La afinada, usamos su tercer armónico (Mi) para afinar la cuerda Mi, y con esta afinada, su armónico para afinar la cuerda Si.
Para afinar el Fa, usaremos el Do como referencia para afinar el tercer armónico de Fa.
En este punto tendríamos nuestro instrumento afinado por quintas justas o naturales. Este sistema se suele denominar afinación pitagórica y aunque pueda parecer muy cabal… tiene ciertas limitaciones musicales con una base física y matemática, que pasamos a explicar a continuación.
La coma pitagórica
Hagamos el siguiente ejercicio: construir 12 quintas seguidas, si tenemos en cuenta las enarmonías, deberemos llegar al mismo punto del que partimos:
La – Mi – Si – Fa# – Do# – Sol# – Re# (enarmónica Mi♭) – Si♭ – Fa – Do – Sol – Re – La
Si cada una de estas quintas la afinamos según el sistema pitagórico (multiplicando por 3/2 la frecuencia de la nota anterior)… no llegamos a un La bien afinado. Es más fácil verlo en una tabla:

Para ir calculando las sucesivas quintas hemos multiplicado cada quinta por 3/2. La intuición nos diría que al hacer doce quintas seguidas y llegar al La deberíamos tener la misma nota (aunque varias octavas por encima). La realidad es que no. Si queremos que este último La suene realmente un La debe tener una frecuencia de 7040Hz, y nos pasamos casi 100Hz. Para que se cierre el ciclo correctamente, esta última quinta debe ser más pequeña que las demás, esta pequeña diferencia se denomina coma pitagórica. Tiene un valor numérico concreto y hay mucha literatura escrita sobre ella, nos quedaremos con la idea básica: superponiendo quintas perfectas hasta llegar a la misma nota, se obtiene una frecuencia que no es la esperada, con lo cual que hay hacer un ajuste en este intervalo para compensar la diferencia.
La razón es puramente matemática: el encadenamiento sucesivo de factores de frecuencia iguales a 3:2 (la quinta) nunca produce un valor que se pueda reducir a la relación 2:1 (la octava); ningún número es al mismo tiempo potencia de 3 y de 2 (salvo el uno).
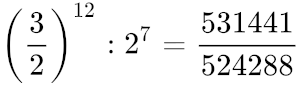
En todos los ejemplos hemos empezado con la nota La porque su frecuencia es un número redondo y simplifica los cálculos, a partir de este momento seguiremos los ejemplos empezando en Do, que es la nota de partida que se ha utilizado tradicionalmente para estudiar los temperamentos.
Mi♭ « Si♭ « Fa « Do » Sol » Re » La » Mi » Si » Fa♯ » Do♯ » Sol♯
La siguiente nota a Sol♯ sería Re♯ (enarmónica de Mi♭). La quinta que se hace más pequeña suele ser la que va de Do♯ a Sol♯, se la suele llamar quinta del lobo.
En el siguiente ejemplo usamos un piano virtual llamado PianoTeq, al seleccionar afinación pitagórica, colocan la quinta del lobo entre el Fa# y el Do#.
Por otra parte, si afinamos todas las notas usando quintas naturales, se producen algunos intervalos que no están muy bien afinados.
La tercera mayor en afinación pitagórica
Si tomamos varias quintas consecutivas desde Do, podemos llegar a la nota Mi, tercera mayor:
Do – Sol – Re – La – Mi
Tenemos este Mi dos octavas por encima. Su frecuencia se puede calculando cuatro quintas consecutivas: (3/2)·(3/2)·(3/2)·(3/2), esto es (3/2)4, que es 81/16 = 5,0625
Si suponemos que Do tiene una frecuencia de 261,63Hz, la frecuencia de este Mi será 261,63 * 5,0625 = 1324,5012Hz. Para poner este Mi en la misma octava que el Do del que partimos, lo dividimos por dos, dos veces consecutivas, obteniendo que Mi = 331,1255Hz
Por otra parte, si atendemos a la serie armónica, sabemos que la tercera mayor es (5/4) de la nota fundamental. Partiendo de Do = 261,63Hz, el Mi sería 261,63*(5/4) = 327,0375
Resumiendo, el Mi que tenemos afinando el sistema pitagórico tiene una frecuencia mayor (331,1255) que el Mi que se obtiene de la serie armónica (327,0375), o dicho de otra forma, la afinación pitagórica genera unas terceras mayores demasiado grandes comparadas con las terceras que se forman naturalmente en la serie armónica.
Parecen unos pocos Hz, pero la diferencia es audible.
¿Cómo afinamos entonces?
Ya hemos visto que la afinación pitagórica es muy atractiva a primera vista, pero presenta dos problemas graves: tiene una quinta muy desafinada y genera terceras mayores algo desafinadas. En las siguientes entregas veremos las posibles soluciones que se han ido proponiendo.

Dejar una contestacion